轰炸（洛谷P1142）
题目描述
“我该怎么办？”飞行员 klux 向你求助。
事实上，klux 面对的是一个很简单的问题，但是他实在太菜了。
klux 要想轰炸某个区域内的一些地方，它们是位于平面上的一些点，但是（显然地）klux 遇到了抵抗，所以 klux 只能飞一次，而且由于飞机比较破，一但起飞就只能沿直线飞行，无法转弯。现在他想一次轰炸最多的地方。
输入格式
第一行一个整数 n。
接下来 n 行，每行有一对整数，表示一个点的坐标。没有一个点会出现两次。
输出格式
一个整数，表示一条直线能覆盖的最多的点数。
输入输出样例
输入 #1复制运行
5 1 1 2 2 3 3 9 10 10 11
输出 #1复制运行
3
说明/提示
数据范围
对于全部数据，保证 1≤n≤700。
本题翻译并改编自 uva270，数据及解答由 uva 提供。
1. 暴力解法：枚举两点定直线 (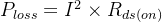
)
核心思路
初学者最容易想到的方法是：
-
两点确定一条直线：我们可以枚举任意两个点i和j，确定一条直线。
-
验证其他点：再遍历剩下的所有点k，判断点k是否在这条直线上。
-
判断共线：利用向量叉积或斜率公式。
-
向量公式：
-
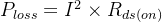
只要等式成立，说明
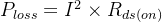三点共线。
-
完整代码
//直接叉积就可以做 如果在一条线上叉积为0
#include
using namespace std;
int n;
typedef pair pii;
pii a[710];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
int x,y;
cin>>x>>y;
a[i].first=x;
a[i].second=y;
}
int ma=0;//最多可以轰炸多少点
//根据两点确定一条直线，我们可以遍历所有固定两点组合的点对，看每种点对最多能覆盖多少个点
for(int i=1;i<=n-2;i++){
for(int j=i+1;j<=n-1;j++){
//由i点和j点确定的点对最多可以轰炸多少个点
//i点和j点肯定可以被轰炸到
int cnt=2;
//i点和j点所组成的向量
pii ij={a[j].first-a[i].first,a[j].second-a[i].second};
for(int k=j+1;k<=n;k++){
//i点和k点所组成的向量
pii ik={a[k].first-a[i].first,a[k].second-a[i].second};
//使用long long防止乘法溢出
if(1ll*ij.first*ik.second==1ll*ij.second*ik.first)
cnt++;
}
ma=max(ma,cnt);
}
}
if(n<=2){//1个点和2个点特判
cout<
痛点分析
这个算法的时间复杂度是O(N^3)。
-
当N=700时，
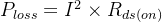，对于 1 秒的时限来说非常勉强（一般 C++ 能跑10^8次运算左右）。 -
实际上这道题数据较弱，或者O(N^3)常数较小，这个暴力解法在洛谷上居然能 AC。
-
但如果N增加到 1000 或 2000，这个方法必死无疑。我们需要更优的解法。
2. 进阶解法：极角排序/斜率统计 ()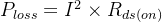
优化思路
我们可以固定一个中心点i，然后看其他点相对于i的斜率。
如果点j和点k相对于i的斜率相同，那么i, j, k三点一定共线。
算法步骤：
-
枚举每一个点i作为“观察点”。
-
计算其他所有点 j (j > i)与i的斜率。
-
为了避免浮点数精度问题，我们用最简分数(dx, dy)来表示斜率。
-
即：
g=gcd(|dx|,|dy|),dx/=g,dy/=g。
-
-
将所有算出来的斜率存入数组，进行排序。
-
排序后，相同的斜率会挨在一起。我们只需要统计最长的一段相同斜率有多少个，就说明有多少个点与i共线。
完整代码
//复杂度：O(N^2 logN)
#include
#include
#include
using namespace std;
//坐标数值可能较大，习惯性开long long，防止中间运算溢出
typedef long long ll;
struct Point {
ll x, y;
}p[710];
int n;
//手写GCD，求最大公约数
ll gcd(ll a,ll b) {
return b==0?a:gcd(b, a%b);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n;
for(int i=0;i>p[i].x>>p[i].y;
// 特判，点数太少的情况，直接全部共线
if(n<=2){
cout<> slopes;
for (int j=i+1;j
3. 总结与对比
| 方法 | 时间复杂度 | 空间复杂度 | 适用范围 | 优点 | 缺点 |
| 暴力枚举 | O(N^3) | O(N) | 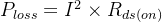| 思路简单，不需要排序 | 数据大时必超时 |
| 斜率排序 | 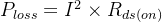| O(N) | 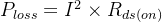| 效率高，利用了排序聚合信息 | 细节多（GCD化简、方向统一） |
关键技巧回顾：
-
避免浮点数：在计算几何中，尽量避免直接计算
k=dy/dx，因为浮点数有精度误差（0.333333!=1/3）。用最简分数(dx, dy)代表斜率是最稳妥的。 -
方向归一化：向量
(1,1)和(-1,-1)虽然方向相反，但在直线上是重合的。我们需要把所有向量都映射到同一个半平面（例如x>0或x=0, y>0的区域），确保它们在排序时被视为“相等”。
