从 1000ms 到 1ms:地理空间邻近查询优化实战
从 1000ms 到 1ms:地理空间邻近查询优化实战
🎯 当 Redis GEORADIUS 撑不住 55 万数据量时,如何实现千倍性能提升?
目录
- 摘要
- 问题背景:Redis GEO 的性能瓶颈
- 核心挑战分析
- 方案演进:从 GeoHash 到 R 树
- 技术方案详解
- 实验结果与效果对比
- 总结与思考
摘要
本文针对天气服务端接入三方数据源时遇到的 大规模地理站点数据的实时邻近查询性能瓶颈 问题,提出一种基于 JTS R 树索引与两阶段筛选策略协同计算的优化方案。
核心成果:
| 指标 | 优化前 (Redis GEO) | 优化后 (R树方案) | 提升倍数 |
|---|---|---|---|
| 平均响应时间 | 1000ms+ | 0.43ms | 2000+倍 |
| 最大 QPS | 受限于慢查询 | 2282+ | 显著提升 |
| 数据规模 | 55万站点 | 55万站点 | - |
核心公式:R树索引 + 两阶段筛选 = 高性能 + 高精度
问题背景:Redis GEO 的性能瓶颈
场景描述
天气服务端需要接入新的三方数据源,核心需求是:根据用户的经纬度,快速找到最近的气象站点。
天气提供商会在全球不同地方建设气象站点,这些气象站点在的位置是固定的,有自己的经纬度,当用户执行定位时,那么会拿到用户的经纬度去天气提供商提供的气象站点列表中搜索出离用户最近的一个气象站点,然后以此获取天气相关信息返回给用户。
这是一个典型的 地理空间邻近查询 问题。
最初的方案:Redis GEO
传统方案采用 Redis GEO 数据结构,使用 GEORADIUS 命令实现:
# Redis GEO 查询最近点
GEORADIUS weather_stations 116.397128 39.916527 10 km WITHDIST COUNT 1 ASC
理论上这个方案很完美:
- ✅ Redis 官方支持,API 简单
- ✅ 基于 Geohash 编码,空间复杂度低
- ✅ 跳表结构,查询复杂度 O(log N)
现实的残酷:上线后的噩梦
当数据量达到 55 万站点 且 QPS 达到一定阈值时,问题爆发了:
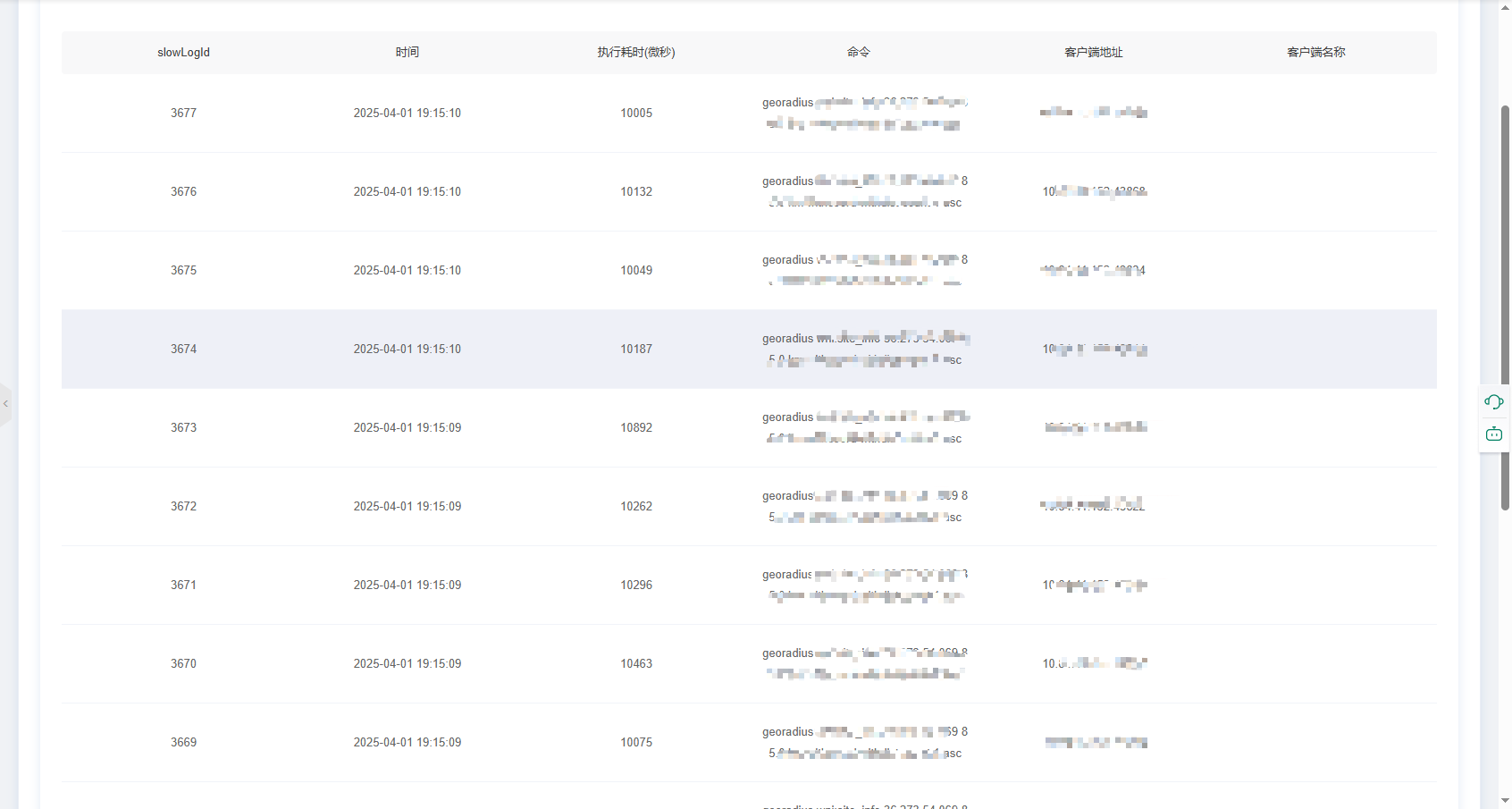
出现大量 10 秒以上的慢查询
核心挑战分析
Redis GEO 为什么会这么慢?
深入分析后,我们发现 Redis GEO 基于 Geohash 编码存在以下缺陷:
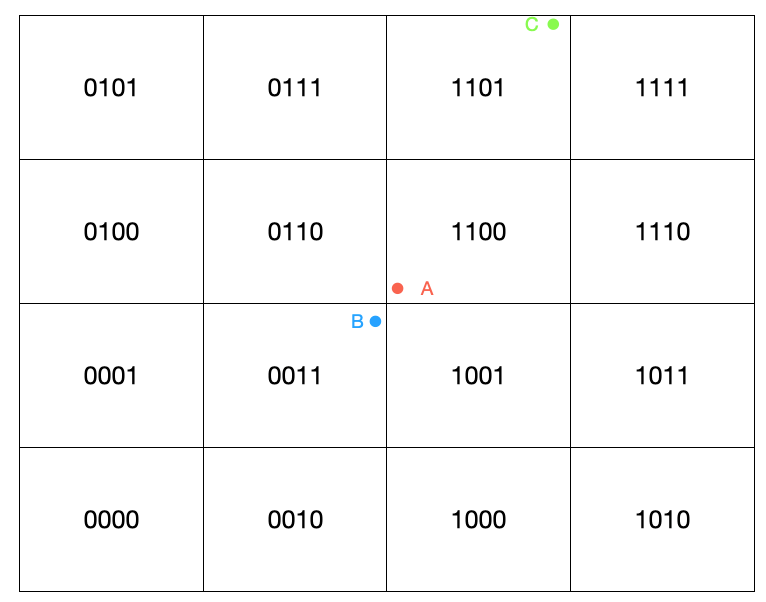
虽然 A 和 C 的 Geohash 编码相近,但实际上 B 距离 A 更近!
这就是 Geohash 的边界问题为了避免这种问题,redis 会先计算出 A 的 东南西北 以及 东北、东南、西北、西南八个区块以及自己身所在的区块,即九宫格区域内所有坐标点,然后计算与当前点的距离,再进一步筛选出符合距离条件的点。
要找出距离 A 最近的点,那么会扫描 0111、1101、1111、0110、1100、11110、0011、1001、1011 九个宫格里的点位列表,然后计算出 A 和每个点位的真实距离,判断哪个点位距离最近。
为了解决边界问题,Redis 必须搜索"九宫格"区域:
| 问题 | 影响 | 严重程度 |
|---|---|---|
| 全表扫描 | 数据密度不均时,单个命令触发跨多网格扫描 | 🔴 严重 |
| 三角函数计算 | 候选集需要球面距离计算,大量 sin/cos 运算 | 🔴 严重 |
| 单线程瓶颈 | Redis 单线程,无法利用多核 CPU | 🔴 严重 |
| 运维复杂 | 需要维护额外的 Redis Sentinel 集群 | 🟡 中等 |
问题本质
问题根源 = Geohash 边界问题 + 球面距离计算开销 + Redis 单线程限制
我们需要一个全新的方案!
方案演进:从 GeoHash 到 R 树
方案一:GeoHash + 二分搜索(失败)
最初的想法: 在应用层复现 Redis GEO 的核心机制
// 方案一:GeoHash + 二分搜索
public class GeoHashIndex {
private List<String> encodedList; // 有序的 GeoHash 编码列表
// 理论上 O(log N) 的时间复杂度
public String findNearest(double lat, double lng) {
String hash = encodeGeoHash(lat, lng);
int idx = Collections.binarySearch(encodedList, hash);
// ....
// ....
return encodedList.get(idx);
}
}
理论优势:
- 🔢 时间复杂度 O(log N),55 万数据约 20 次比较
- ⚡ 数据量大时也可以分片,然后并行处理多个子区间,最终多路归并
💣 关键问题: 简单的 GeoHash 排序搜索 无法精确找到邻近点!和 Redis 一样需要处理边界问题,实现复杂度极高。
方案二:R 树索引(成功)
在深入研究后,我们发现了一个更优雅的解决方案——R 树(R-tree)
什么是 R 树?
R 树是将 B 树扩展到多维情况的数据结构,由 Antonin Guttman 于 1984 年提出。
┌─────────────────────────────────────────────────────────────┐
│ R 树结构示意图 │
├─────────────────────────────────────────────────────────────┤
│ │
│ ┌───────┐ │
│ │ Root │ │
│ └───┬───┘ │
│ ┌───────────┼───────────┐ │
│ ▼ ▼ ▼ │
│ ┌───────┐ ┌───────┐ ┌───────┐ │
│ │ R1 │ │ R2 │ │ R3 │ ← 大矩形区域 │
│ └───┬───┘ └───┬───┘ └───┬───┘ │
│ │ │ │ │
│ ┌───┴───┐ ┌───┴───┐ ┌───┴───┐ │
│ ▼ ▼ ▼ ▼ ▼ ▼ │
│ ┌───┐ ┌───┐ ... ← 小矩形/点 │
│ │p1 │ │p2 │ │
│ └───┘ └───┘ │
│ │
│ 核心思想:通过大矩形递归寻找小矩形,直到叶子节点 │
│ │
└─────────────────────────────────────────────────────────────┘
R 树的优势
| 特性 | 说明 | 收益 |
|---|---|---|
| 层次化索引 | 通过 MBB(最小边界矩形)实现空间聚类 | 快速剪枝 |
| 动态平衡 | 自动适应数据分布变化 | 无需手动调优 |
| 精确剪枝 | 通过空间关系快速排除无效候选 | 减少计算量 |
| 时间复杂度 | O(log N),55 万数据最多 20 次查询 | 极致性能 |
技术方案详解
整体架构
┌─────────────────────────────────────────────────────────────┐
│ 地理空间邻近查询优化方案 │
├─────────────────────────────────────────────────────────────┤
│ │
│ ┌─────────────────┐ ┌─────────────────┐ │
│ │ 📦 数据预热 │ │ 🌲 R树索引 │ │
│ │ Kryo序列化 │───▶│ STRtree构建 │ │
│ │ (~300ms) │ │ (~1s) │ │
│ └─────────────────┘ └────────┬────────┘ │
│ │ │
│ ▼ │
│ ┌─────────────────────────┐ │
│ │ 🔍 两阶段筛选策略 │ │
│ ├─────────────────────────┤ │
│ │ 阶段1: 平面距离粗筛 │ │
│ │ 55万 → K个候选点 │ │
│ ├─────────────────────────┤ │
│ │ 阶段2: 球面距离精算 │ │
│ │ K个 → 1个最近点 │ │
│ └─────────────────────────┘ │
│ │ │
│ ▼ │
│ ⚡ 平均 0.43ms 响应 │
│ │
└─────────────────────────────────────────────────────────────┘
第一步:冷启动优化(数据预热)
问题: 业务启动时需要将 55 万站点数据加载到内存构建 R 树索引。
解决方案: 使用 Kryo 二进制序列化实现快速加载。
数据流向:MySQL → Kryo二进制文件 → 内存加载 → R树构建
private List<WniSiteInfoDO> readFromBinary() throws FileNotFoundException {
log.info(" 二进制文件读取开始");
long startTime = System.currentTimeMillis();
List<WniSiteInfoDO> sites = new ArrayList<>();
try (Input input = new Input(Objects.requireNonNull(
getClass().getClassLoader().getResourceAsStream("sites.bin")))) {
Kryo kryo = new Kryo();
kryo.register(WniSiteInfoDO.class); // 保持与序列化时相同的注册方式
int cnt = 0;
try {
while (true) { // 通过无限循环持续读取
WniSiteInfoDO site = kryo.readObject(input, WniSiteInfoDO.class);
sites.add(site);
cnt++;
// 保持与导出一致的进度输出节奏
if (cnt % 1000 == 0) {
double progress = cnt * 100.0 / sites.size(); // 动态计算进度
log.info(" 加载进度: 第 {} 条记录", cnt);
}
}
} catch (KryoException e) {
// ....
}
性能数据:
- 📦 55 万条数据
- ⏱️ 加载耗时:~300ms
- 💡 无需拆分文件,性能已足够
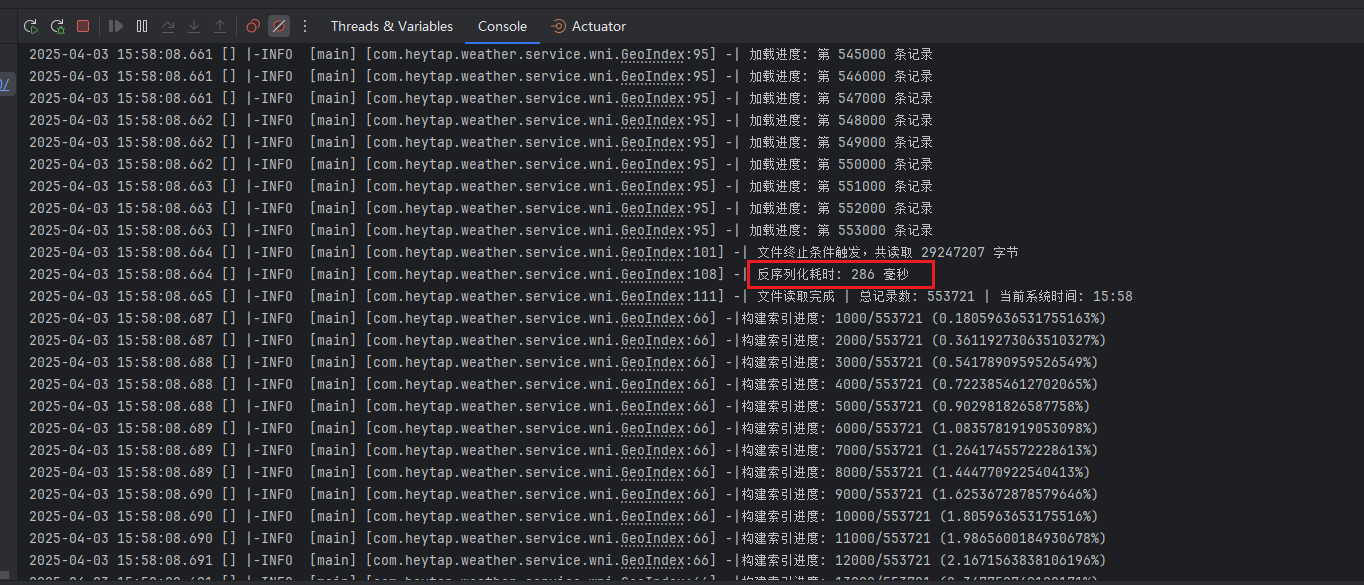
第二步:空间索引构建
使用 JTS 库的 STRtree(R 树变种)构建空间索引:
private final STRtree index;
private void loadAllSites() {
List<WniSiteInfoDO> sites = null;
try {
sites = readFromBinary();
} catch (FileNotFoundException e) {
log.error(" 二进制文件读取失败", e);
throw new RuntimeException(e);
}
// 构建R树索引
int cnt = 0;
int total = sites.size();
for (WniSiteInfoDO site : sites) {
Coordinate coord = new Coordinate(site.getLng(), site.getLat());
Point point = geometryFactory.createPoint(coord);
point.setUserData(site);
index.insert(point.getEnvelopeInternal(), point);
cnt++;
if (cnt % 1000 == 0) {
log.info("构建索引进度: {}/{} ({}%)", cnt, total, cnt * 100.0 / total);
}
}
log.info("开始构建R树...");
index.build();
log.info("R树构建完成,共索引 {} 个站点", total);
log.info("Geo索引构建完成,站点数量:{}", sites.size());
}
构建性能:
- 🌲 55 万站点
- ⏱️ 构建耗时:~1s
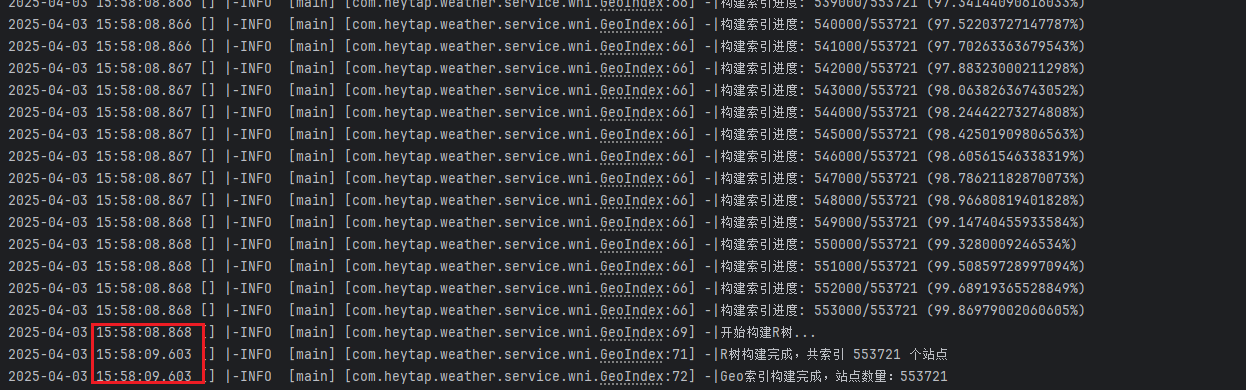
第三步:两阶段筛选策略(核心!)
🔑 关键洞察: R 树使用 平面笛卡尔坐标系 计算距离,但地球表面是 椭球面。直接使用会导致结果失真!
解决方案:两阶段筛选协同计算
┌─────────────────────────────────────────────────────────────┐
│ 两阶段筛选策略 │
├─────────────────────────────────────────────────────────────┤
│ │
│ 阶段一:粗筛(R树 + 平面距离) │
│ ┌─────────────────────────────────────────────────────┐ │
│ │ 输入: 目标点 (lat, lng) │ │
│ │ 处理: R树快速检索平面距离最近的 K 个候选点 │ │
│ │ 输出: K 个候选点 (如 K=10) │ │
│ │ 效果: 55万 → 10个,排除 99.998% 无关点 │ │
│ │ 特点: 🚀 极快,但有误差 │ │
│ └─────────────────────────────────────────────────────┘ │
│ │ │
│ ▼ │
│ 阶段二:精算(Haversine 球面距离) │
│ ┌─────────────────────────────────────────────────────┐ │
│ │ 输入: K 个候选点 │ │
│ │ 处理: 使用 Haversine 公式计算真实球面距离 │ │
│ │ 输出: 1 个最近点 │ │
│ │ 效果: 10个 → 1个,找到精确最近点 │ │
│ │ 特点: 🎯 精确,计算量可控 │ │
│ └─────────────────────────────────────────────────────┘ │
│ │
└─────────────────────────────────────────────────────────────┘
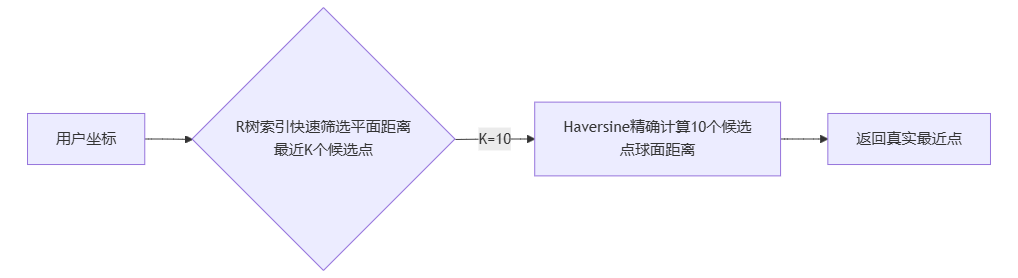
为什么这个策略有效?
| 阶段 | 方法 | 优点 | 缺点 | 数据量 |
|---|---|---|---|---|
| 粗筛 | 平面距离 | 极快 (O(log N)) | 有误差 | 55万 → 10 |
| 精算 | Haversine | 精确 | 需要三角函数 | 10 → 1 |
核心思想:用快速但不完全准确的方法排除大部分无关数据,再用精确方法处理少量候选。
Haversine 公式
/**
* Haversine公式计算距离(单位:米)
*/
private double haversine(double lat1, double lon1, double lat2, double lon2) {
int R = 6371000; // 地球半径(米)
double phi1 = Math.toRadians(lat1);
double phi2 = Math.toRadians(lat2);
double deltaPhi = Math.toRadians(lat2 - lat1);
double deltaLambda = Math.toRadians(lon2 - lon1);
double a = Math.sin(deltaPhi / 2) * Math.sin(deltaPhi / 2) +
Math.cos(phi1) * Math.cos(phi2) *
Math.sin(deltaLambda / 2) * Math.sin(deltaLambda / 2);
double c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));
return R * c;
}
完整查询流程
/**
* 获取最近邻的点
*
*/
public WniSiteInfoDO findNearest(double lat, double lng) {
try {
Coordinate userCoord = new Coordinate(lng, lat);
Point userPoint = geometryFactory.createPoint(userCoord);
// 使用GeometryItemDistance计算真实几何距离
ItemDistance distanceCalculator = new GeometryItemDistance();
// 获取最近的10个候选点(平面坐标系和球面坐标系之间存在误差,所以多选择几个点用来控制误差)
// 初筛阶段
Object[] candidates = index.nearestNeighbour(
userPoint.getEnvelopeInternal(),
userPoint,
distanceCalculator,
10
);
// 细筛阶段
return Arrays.stream(candidates)
.map(geometry -> (Geometry) geometry)
.map(geom -> (WniSiteInfoDO) geom.getUserData())
.min((s1, s2) ->
Double.compare(
haversine(lat, lng, s1.getLat(), s1.getLng()),
haversine(lat, lng, s2.getLat(), s2.getLng())
)
)
.orElse(null);
} catch (Exception e) {
log.error("WNI R树查询失败!", e);
return null;
}
}
实验结果与效果对比
压测数据
启用多个线程进行压测,在总查询数22846下,QPS高达2282.32的情况下,平均响应时间为0.43ms,性能远高于Redis GEO结构下的最近邻点计算
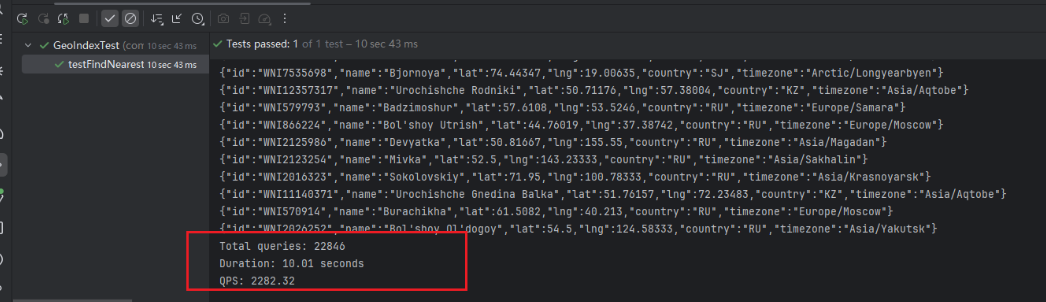
方案对比
| 方案 | 平均响应时间 | 最大 QPS | 稳定性 | 运维复杂度 |
|---|---|---|---|---|
| Redis GEO | 1000ms+ (含慢查询) | 受限 | ❌ 频繁告警 | 🟡 需要维护 Redis 集群 |
| R树方案 | 0.43ms | 2282+ | ✅ 稳定 | ✅ 应用内存,无额外依赖 |
性能提升
性能提升倍数 = 1000ms / 0.43ms ≈ 2,300+ 倍 🚀
实际效果:从秒级响应优化到毫秒级,成功支撑高并发场景!
总结与思考
我们学到了什么
-
不要迷信"银弹"方案
- Redis GEO 在小数据量下表现优秀
- 但在特定场景(大数据量 + 高并发)下可能成为瓶颈
-
理解底层原理很重要
- 了解 Geohash 的边界问题,才能理解 Redis GEO 的局限性
- 了解 R 树的空间索引原理,才能设计出正确的优化方案
-
Trade-off 思维
- 两阶段筛选策略是典型的 速度 vs 精度 的权衡
- 用"近似快速"处理大量数据,用"精确慢速"处理少量数据
核心设计思想
┌─────────────────────────────────────────────────────────────┐
│ │
│ R树层次索引 + 两阶段筛选 = 高性能 + 高精度 │
│ ↓ ↓ │
│ 快速空间剪枝 粗筛 + 精算 │
│ │
└─────────────────────────────────────────────────────────────┘
方案总结
| 组件 | 技术选型 | 作用 |
|---|---|---|
| 数据加载 | Kryo 序列化 | 快速冷启动 (~300ms) |
| 空间索引 | JTS STRtree | O(log N) 快速检索 |
| 粗筛阶段 | 平面距离 | 排除 99.99% 无关点 |
| 精算阶段 | Haversine | 确保结果精度 |
适用场景
这套方案适用于:
- ✅ 大规模地理站点数据(万级以上)
- ✅ 高并发邻近查询场景
- ✅ 对响应时间有严格要求的服务
本文基于天气服务端真实优化案例编写,成功助力俄罗斯大区接入三方数据源。
作者注:性能优化的关键不是使用最复杂的技术,而是选择最适合场景的方案。Redis GEO 是优秀的工具,但在特定场景下,基于应用层的空间索引可能是更好的选择。理解问题本质,才能找到最佳解法。
Happy Coding! 🚀