机器学习————K-Means 聚类
一、核心概念
K-Means 是一种无监督学习的聚类算法，核心目标是将 n 个样本划分为 k 个不重叠的簇，使得每个簇内的样本尽可能相似，也就是簇内距离最小。同样，不同簇的样本尽可能不同，也就是簇间距离最大。
概念解读：
- 簇：具有相似特征的样本集合，最终聚类结果的基本单位。
- 质心：每个簇的 “中心”，是该簇所有样本特征的均值向量。
- 距离度量：最常用欧几里得距离，也可使用曼哈顿距离等其它距离计算公式，用于衡量样本与质心的相似度，距离越小越相似。
- 核心流程：
- 初始化：随机选择
k个样本作为初始质心； - 分配：计算每个样本到所有质心的距离，将样本分配给距离最近的质心所属簇；
- 更新：重新计算每个簇的质心，取簇内所有样本的特征均值；
- 收敛：重复 “分配 - 更新” 步骤，直到质心不再显著变化或达到最大迭代次数。
- 初始化：随机选择
- 损失函数：也叫 “惯性值”，表示所有样本到其所属簇质心的平方距离之和，目标是最小化该值。
二、计算原理
1.距离公式——易欧几里得距离为例
假设样本为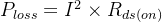
,d为特征维度和质心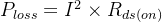，两者的欧几里得距离为：
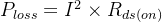
2.目标函数
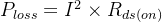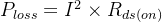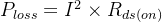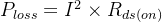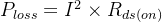设样本集合为 ，聚类结果为 ， 是第j个簇的样本集合， 是 的质心。
则目标函数为：
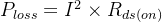
K-Means 的核心是通过迭代最小化 J。
3.质心更新公式
第 j 个簇的质心是该簇所有样本的特征均值：
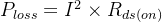
其中 ∣Cj∣ 是第 j 个簇的样本数量。
三、代码解释
模块一：导入必要库
import numpy as np#计算核心库
import matplotlib.pyplot as plt # 用于可视化聚类结果
模块二：定义 K-Means 核心类
#定义K-Means聚类核心类
class KMeans:
# 类的初始化方法（创建实例时执行，设置超参数和核心变量）
def __init__(self, n_clusters=2, max_iter=300, tol=1e-4):
"""
K-Means模型初始化函数
:param n_clusters: 聚类数量k（默认值2）
:param max_iter: 最大迭代次数（默认值300，防止无限循环）
:param tol: 质心收敛阈值（默认值1e-4，质心变化小于该值则停止迭代）
"""
# 保存聚类数量k到实例属性
self.n_clusters = n_clusters
# 保存最大迭代次数到实例属性
self.max_iter = max_iter
# 保存收敛阈值到实例属性
self.tol = tol
# 初始化质心变量（后续训练中赋值，形状为(k, 特征维度)）
self.centroids = None
# 初始化样本标签变量（后续训练中赋值，形状为(样本数量,)）
self.labels = None
# 定义私有方法：计算欧几里得距离（向量化实现，支持批量计算）
def _euclidean_distance(self, x1, x2):
"""
计算样本矩阵与质心矩阵的欧几里得距离（批量计算，避免循环）
:param x1: 样本矩阵，形状为(n_samples, n_features)
:param x2: 质心矩阵，形状为(n_clusters, n_features)
:return: 距离矩阵，形状为(n_samples, n_clusters)
"""
# x1[:, np.newaxis]：将样本矩阵扩展维度为(n_samples, 1, n_features)
# 与质心矩阵x2(n_clusters, n_features)广播运算，相减后平方
# axis=2：沿特征维度求和，得到平方距离
# np.sqrt：开平方得到最终欧几里得距离
return np.sqrt(np.sum((x1[:, np.newaxis] - x2) ** 2, axis=2))
# 定义模型训练方法（核心：实现K-Means迭代流程）
def fit(self, X):
"""
训练K-Means模型，完成聚类
:param X: 输入样本矩阵，形状为(n_samples, n_features)
"""
# 获取样本数量（n_samples）和特征维度（n_features）
n_samples, n_features = X.shape
# 随机选择k个不重复的样本索引（replace=False：不重复采样）
random_idx = np.random.choice(n_samples, self.n_clusters, replace=False)
# 初始化质心：将选中的k个样本作为初始质心
self.centroids = X[random_idx]
# 开始迭代（最多迭代max_iter次）
for _ in range(self.max_iter):
# 子步骤1：计算所有样本到所有质心的距离（得到距离矩阵）
distances = self._euclidean_distance(X, self.centroids)
# 子步骤2：为每个样本分配聚类标签
# np.argmin：沿axis=1（行）取最小值的索引，即距离最近的质心编号
# 结果形状为(n_samples,)，每个元素是样本所属的簇编号（0~k-1）
self.labels = np.argmin(distances, axis=1)
# 子步骤3：初始化新质心矩阵（形状与原质心一致，初始值全0）
new_centroids = np.zeros((self.n_clusters, n_features))
# 遍历每个簇，计算新质心
for j in range(self.n_clusters):
# 筛选出第j个簇的所有样本（self.labels == j：布尔索引）
cluster_samples = X[self.labels == j]
# 防止空簇（随机初始化可能导致某个簇无样本）
if len(cluster_samples) > 0:
# 计算簇内样本的特征均值（axis=0：沿样本维度求均值）
# 结果作为第j个簇的新质心
new_centroids[j] = np.mean(cluster_samples, axis=0)
# 子步骤4：判断是否收敛（质心变化小于阈值则停止）
# 计算每个质心的位移（欧几里得距离），再求和得到总位移
centroid_shift = np.sum(np.sqrt(np.sum((new_centroids - self.centroids) ** 2, axis=1)))
# 如果总位移小于收敛阈值，说明质心稳定，停止迭代
if centroid_shift < self.tol:
break
# 未收敛则更新质心：将新质心赋值给实例属性
self.centroids = new_centroids
模块三：生成模拟测试数据
#定义测试数据生成函数
def generate_test_data(n_samples=300, n_clusters=3, random_state=42):
"""
生成模拟的二维聚类测试数据
:param n_samples: 总样本数量（默认300）
:param n_clusters: 聚类数量（默认3）
:param random_state: 随机种子（固定种子保证结果可复现）
:return: 测试数据矩阵，形状为(n_samples, 2)
"""
# 设置随机种子，确保每次运行生成的随机数相同
np.random.seed(random_state)
# 定义3个簇的真实中心（二维坐标）
centers = np.array([[0, 0], [5, 5], [0, 5]])
# 初始化空列表，存储每个簇的样本
data = []
# 遍历每个簇的真实中心
for center in centers[:n_clusters]:
# 生成围绕中心的正态分布样本：
# np.random.randn：生成标准正态分布随机数（均值0，方差1）
# *0.8：缩小噪声范围，让样本更集中在中心周围
# +center：将样本中心平移到指定位置
cluster_data = center + np.random.randn(n_samples // n_clusters, 2) * 0.8
# 将当前簇的样本添加到列表
data.append(cluster_data)
# 将列表中的多个簇样本合并为一个矩阵（vstack：垂直堆叠）
data = np.vstack(data)
# 打乱样本顺序（避免样本按簇排列，模拟真实数据分布）
np.random.shuffle(data)
# 返回生成的测试数据
return data
模块四：测试 K-Means 模型并可视化
if __name__ == "__main__":
# 生成测试数据：300个样本，3个簇，固定随机种子
X = generate_test_data(n_samples=300, n_clusters=3)
# 初始化K-Means模型：指定3个簇，最大迭代300次，收敛阈值1e-4
kmeans = KMeans(n_clusters=3, max_iter=300, tol=1e-4)
# 训练模型：传入测试数据，完成聚类
kmeans.fit(X)
# 可视化结果
plt.figure(figsize=(8, 6))
# 绘制样本，按聚类标签着色
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels, cmap='viridis', alpha=0.7, s=50)
# 绘制质心（红色大圆点）
plt.scatter(kmeans.centroids[:, 0], kmeans.centroids[:, 1], c='red', marker='X', s=200, label='Centroids')
plt.title('K-Means Clustering Result')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
# 输出关键信息
print("最终质心坐标：")
for i, centroid in enumerate(kmeans.centroids):
print(f"簇 {i+1} 质心：{centroid.round(2)}")
print(f"样本聚类标签（前10个）：{kmeans.labels[:10]}")
运行结果
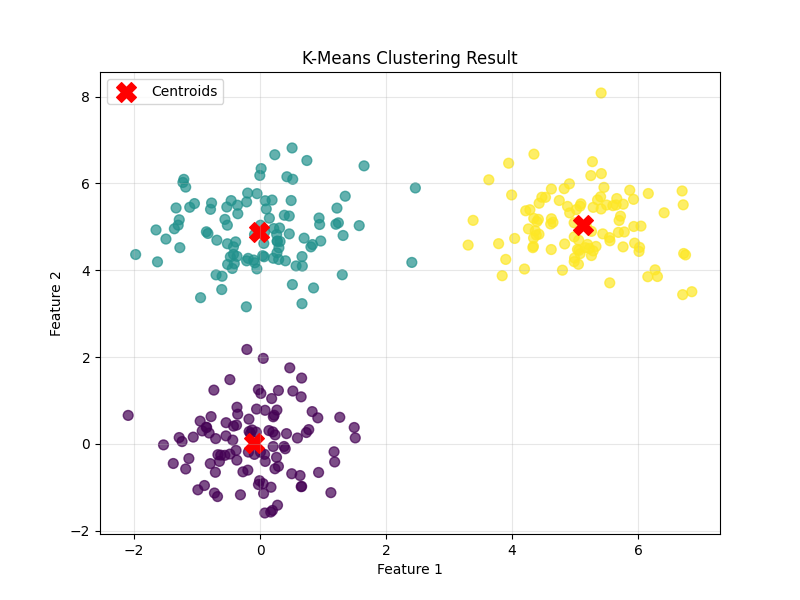
结论：成功将二维数据划分为 3 个结构清晰的簇，每个簇的质心准确反映了该簇的中心位置，是无监督聚类任务中典型的有效结果。
最终质心坐标：
簇 1 质心：[-0.09 0.03]
簇 2 质心：[-0.01 4.89]
簇 3 质心：[5.13 5.04]
样本聚类标签（前10个）：[0 0 1 2 0 0 1 0 0 2]
四、结语
- 核心逻辑：K-Means 通过 “随机初始化质心→分配样本到最近质心→更新簇质心→判断收敛” 的迭代流程，最小化簇内样本到质心的平方距离和；
- 数学核心：欧几里得距离——衡量相似度、质心均值公式——更新中心、惯性值——损失函数；
- 代码关键：向量化计算——避免循环提升效率、收敛判断——防止无效迭代、空簇处理——提升鲁棒性。
K-Means 优点是简单高效、易实现；缺点是需要预先指定 k、对初始质心敏感、对异常值鲁棒性差，实际使用中可结合 “肘部方法” 选择最优 k，或用 K-Means++ 优化初始质心。
感谢大家的观看！如果有不足，期待大家的批评指正。
