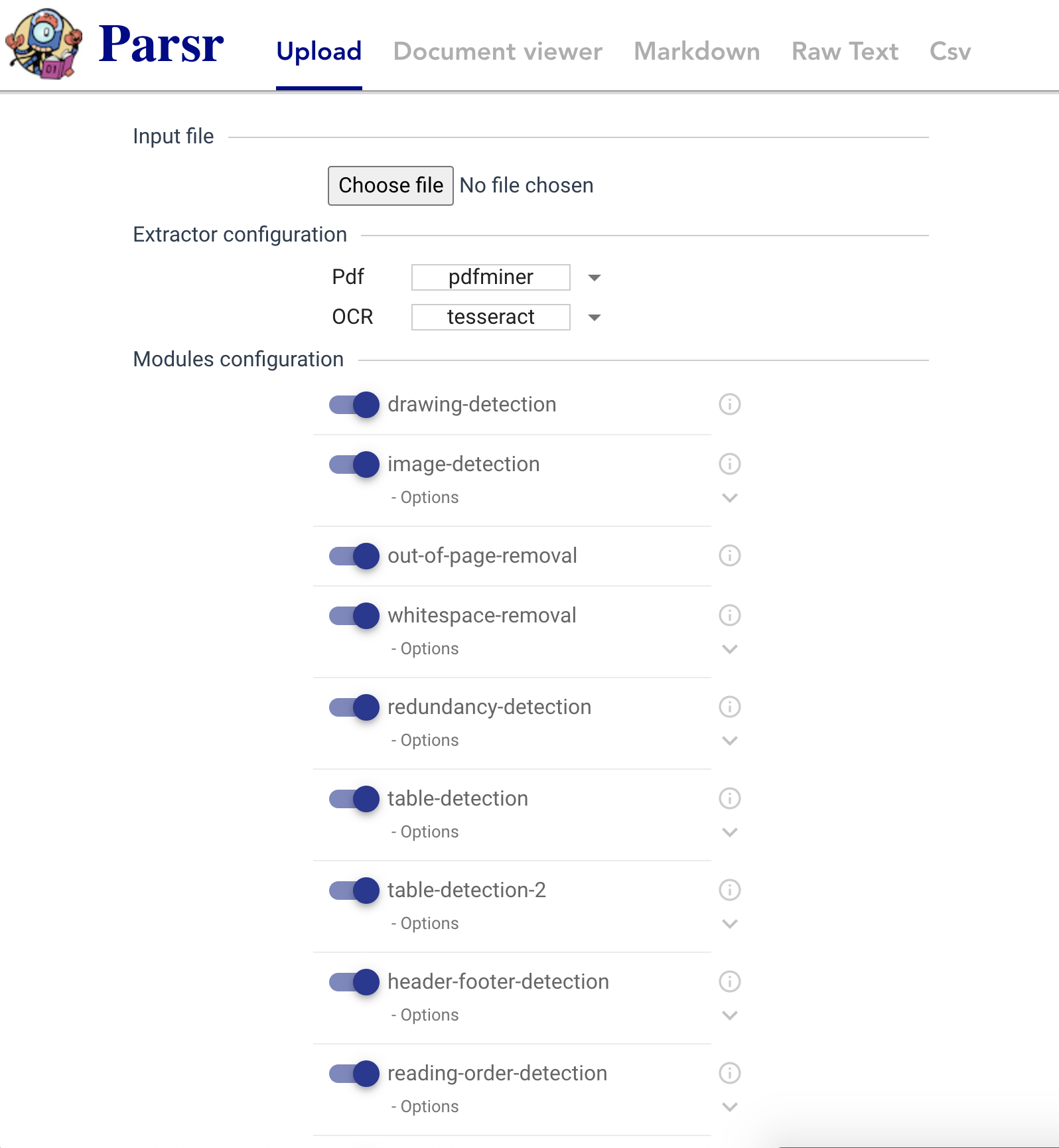
DFS模板及例题解析
深度优先搜索(Depth-First Search,DFS)是一种用于遍历或搜索树或图的算法。其核心思想是尽可能深地探索分支,直到无法继续为止,再回溯到上一个节点继续探索。
1. 简单模板
void dfs(...)
{
//1.中止条件
//2.访问该点并dfs
//注意回溯
}2. 例题
例题一:排列数字
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1C ++ 代码:
#include
using namespace std;
int n;
//记录不同的数字排列
int path[8];
//用于记录是否访问过
bool st[8];
void dfs(int u)
{
//dfs中止条件,即遍历到最底时输出此时数字排列
if(u == n)
{
for(int i = 0; i < n; i ++) cout << path[i] << " ";
cout << endl;
return;
}
//这一次可有1~n种可能
for(int i = 1; i <= n; i ++)
{
//要去掉已访问过的
if(!st[i])
{
st[i] = true;
path[u] = i;
//进行dfs遍历下一层
dfs(u + 1);
st[i] = false;
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
} 例题二:N皇后问题(困难)
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
C ++ 代码:
#include
using namespace std;
const int N = 100;
int n;
//存储要输出的棋子摆法
char g[N][N];
//cal用于记录当前列没有棋子
//p用于记录当前斜线上没有棋子
//dp用于记录当前反斜线上没有棋子
//当前行不用记录,因为就是按行遍历的,一行遍历一次
bool cal[N], p[N], dp[N];
void dfs(int u)
{
//中止条件,当遍历序号等于棋子行数时,说明到底过了
if(u == n)
{
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < n; j ++)
{
cout << g[i][j];
}
cout << endl;
}
cout << " " << endl;
}
else{
for(int i = 0; i < n; i ++)
{
//不处于同一行、同一列或同一斜线上则放皇后
if(!cal[i] && !p[i + u] && !dp[u - i + n])
{
cal[i] = p[i + u] = dp[u - i + n] = true;
g[u][i] = 'Q';
//dfs下一行
dfs(u + 1);
//回溯
cal[i] = p[i + u] = dp[u - i + n] = false;
g[u][i] = '.';
}
}
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < n; j ++)
{
g[i][j] = '.';
}
}
dfs(0);
return 0;
} 例题三:递归实现指数型枚举
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1≤n≤15
输入样例:
3
输出样例:
3
2
2 3
1
1 3
1 2
1 2 3C ++ 代码:
#include
using namespace std;
const int N = 20;
//记录状态,是否选择当前数。选1,不选0
int state[N];
int n;
void dfs(int u)
{
if(u > n)
{
for(int i = 1; i <= n; i ++)
{
if(state[i] == 1) cout << i << " ";
}
cout << endl;
return;
}
//选择当前数
state[u] = 1;
dfs(u + 1);
//不选当前数
state[u] = 0;
dfs(u + 1);
}
int main()
{
cin >> n;
dfs(1);
return 0;
} 例题四:递归实现组合型枚举
从 1∼n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。
输入格式
两个整数 n,m ,在同一行用空格隔开。
输出格式
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行内的数升序排列,相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如 1 3 5 7 排在 1 3 6 8 前面)。
数据范围
n>0 ,
0≤m≤n ,
n+(n−m)≤25
输入样例:
5 3
输出样例:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5 C ++ 代码:
#include
using namespace std;
const int N = 30;
int n, m;
//表示这次选不选
int state[N];
//u表示选第几个数,start表示从几开始
void dfs(int u, int start)
{
if(u > m)
{
for(int i = 1; i <= n; i ++)
{
if(state[i] == 1) cout << i << " ";
}
cout << endl;
return;
}
//当剩余还可以选的字数大于要求选的数量减去已选的数量时,有两种选择,选或不选
if(n - start + 1 > m - u + 1)
{
state[start] = 1;
dfs(u + 1, start + 1);
state[start] = 0;
dfs(u, start + 1);
}
//当剩余还可以选的字数等于要求选的数量减去已选的数量时,这时剩下的都得选
else if(n - start + 1 == m - u + 1)
{
state[start] = 1;
dfs(u + 1, start + 1);
state[start] = 0;
}
//当剩余还可以选的字数小于要求选的数量减去已选的数量时,不能满足要求,结束
else return;
}
int main()
{
cin >> n >> m;
dfs(1, 1);
return 0;
} 例题五:水塘数量
洛谷题目链接
C ++代码:
#include
using namespace std;
const int N = 110;
char g[N][N];
int n, m;
//这里不要用st来标记是否被访问,容易超内存,就把访问过的都设置为'T'就好
//bool st[N][N];
//用于遍历相邻水坑
int dx[8] = {0, -1, 0, 1, -1, -1, 1, 1};
int dy[8] = {1, 0, -1, 0, -1, 1, 1, -1};
void dfs(int x, int y)
{
//把当前设置为'T'表明访问过了
g[x][y] = 'T';
for(int i = 0; i < 8; i ++)
{
int nx = x + dx[i];
int ny = y + dy[i];
//相邻节点存在且为水坑说明相邻
if(nx >= 0 && nx < n && ny >= 0 && ny < m && g[nx][ny] == 'W')
{
dfs(nx, ny);
}
}
}
int main()
{
cin >> n >> m;
int ans = 0;
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < m; j ++) cin >> g[i][j];
}
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < m; j ++)
{
//每次遇到水坑肯定未被遍历(因为遍历的都置T)
if(g[i][j] == 'W')
{
ans ++;
dfs(i, j);
}
}
}
cout << ans;
return 0;
} 例题六:不同路径数
给定一个 n×m 的二维矩阵,其中的每个元素都是一个 [1,9] 之间的正整数。
从矩阵中的任意位置出发,每次可以沿上下左右四个方向前进一步,走过的位置可以重复走。
走了 k 次后,经过的元素会构成一个 (k+1) 位数。
请求出一共可以走出多少个不同的 (k+1) 位数。
输入格式
第一行包含三个整数 n,m,k。
接下来 n 行,每行包含 m 个空格隔开的整数,表示给定矩阵。
输出格式
输出一个整数,表示可以走出的不同 (k+1) 位数的个数。
数据范围
对于 30% 的数据, 1≤n,m≤2,0≤k≤2
对于 100% 的数据,1≤n,m≤5,0≤k≤5,m×n>1
输入样例:
3 3 2
1 1 1
1 1 1
2 1 1
输出样例:
5
样例解释
一共有 5 种可能的 3 位数:
111
112
121
211
212C ++ 代码:
#include
#include
#include
using namespace std;
const int N = 10;
int n, m, k;
char g[N][N];
//定义一个哈希表用于去重
unordered_map h;
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
void dfs(int u, int i, int j, string path)
{
path += g[i][j];
if(u == k)
{
//只要path一样都置为1表示这种路径已存在
h[path] = 1;
return;
}
for(int k = 0; k < 4; k ++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m)
{
dfs(u + 1, x, y, path);
}
}
}
int main()
{
cin >> n >> m >> k;
string path;
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < m; j ++) cin >> g[i][j];
}
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < m; j ++)
{
dfs(0, i, j, path);
}
}
cout << h.size();
return 0;
}