【数据结构】顺序表（下）笔试题 超级详细!!
谁懂啊！顺序表真的是编程面试里的“常驻嘉宾”，但也是好多小伙伴的“痛点盲区”😫！ 明明是数据结构入门级知识点，可一到笔试题里，边界值判断、增删改查优化、时间复杂度把控这些坑，总能让人栽跟头！其实顺序表笔试看似花样多，核心考点就那么几个，摸清套路就能轻松拿捏～ 今天这篇就来扒一扒顺序表笔试题的高频考点、避坑指南和解题技巧，帮你搞定基础题不丢分，进阶题有思路，面试时面对顺序表相关题目再也不慌啦！
目录
一、顺序表的笔试题
1.原地修改类：
1.1思路：
1.2题目
1.2.1题目要求：
1.2.2核心考点：
1.2.3解题思路：
1.2.4完整代码：
2.合并两个有序数组：
2.1思路：
2.2题目：
2.2.1题目要求：
2.2.2解题思路：
2.2.3完整代码：
二、对顺序表的思考
一、顺序表的笔试题
1.原地修改类：
1.1思路：
原地修改类题目（移除、去重）优先使用双指针（快慢指针），实践复杂度为O（n），空间复杂度为O(1）
1.2题目
1.2.1题目要求：
给定一个数组 nums 和一个值 val ，原地移除所有数值等于 val 的元素，要求不能使用额外的数组空间，空间复杂度必须为 O(1)。
1.2.2核心考点：
双指针法的应用、边界条件处理、原地修改的空间优化。
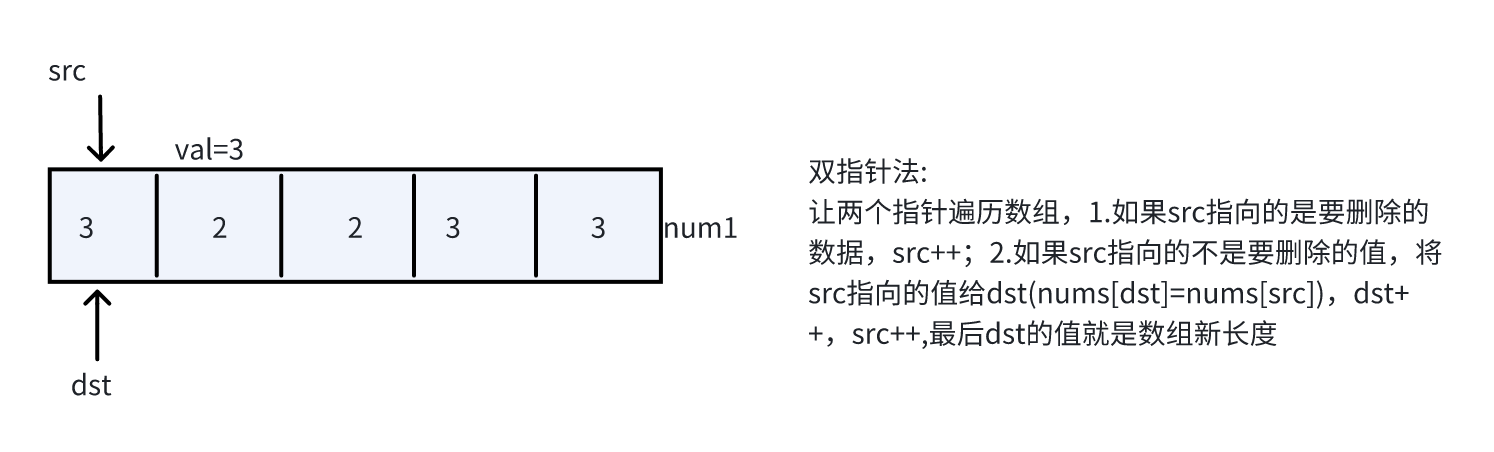
1.2.3解题思路：
用快慢指针（ src 和 dst ）遍历数组，快指针src负责扫描，慢指针dst负责写入，遇到非目标值时就复制到慢指针位置，最终慢指针的位置就是新数组的有效长度。
1.2.4完整代码：
#define N 5
//参数：nums-原数组，val-要移除的元素，numsize-数组原始长度
int RemoveElement(int *nums,int val,int numsize)
{
int src = 0;//快指针遍历整个数组
int dst = 0;//慢指针指向新数组的下一个写入位置
while(dst < numsize)
{
if(nums[src] == val)
{ src++;}
else
{
nums[dst]=nums[src];
dst++;
src++;
}
}
return dst;//慢指针的位置就是新数组的有效长度
}
int main()
{
int nums[N]={0};
for(int i = 0;i < N;i++)
{
scanf("%d",&nums[i]");
}
int length = sizeof(nums)/sizeof(nums[0]);//计算有效数据个数
printf("原数组长度：
");
it val = 0;
printf("请输入要删除的数值：
");
scanf("%d",&val);
length = RemoveElement(nums,val,length);
printf("新的数组长度为：
");
printf("%d",length);
return 0;
}2.合并两个有序数组：
2.1思路：
合并有序顺序表用双指针分别遍历两个表，依次比较取较小值，避免嵌套循环（时间复杂度O(n+m)才是合格解）；
2.2题目：
2.2.1题目要求：
给你两个非递减顺序排列的整数数组nums1,nums2，另有两个整数m和n分别表示nums1和nums2中的元素数目，请你合并nums2到nums1中，使合并后的数组同样是非递减顺序
2.2.2解题思路：
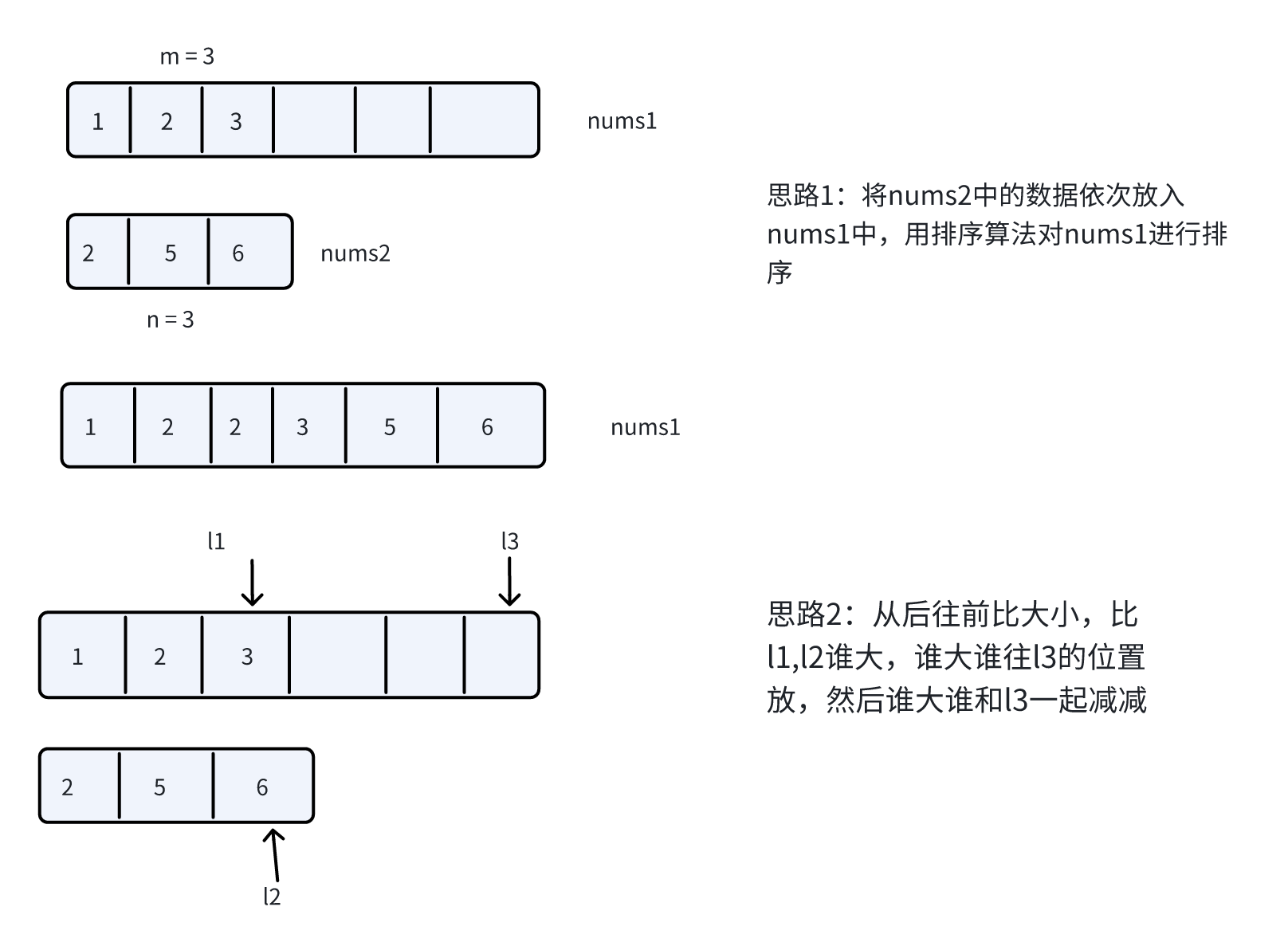
从两个数组的末尾（ l1 = m-1 ， l2 = n-1 ）开始比较，把较大的元素放到 nums1 的末尾空闲位置（ l3 = m+n-1 ）。
这样避免了从前向后合并时需要移动元素的问题，是原地合并的最优解。
当其中一个数组遍历完后，把另一个数组剩余的元素直接复制到 nums1 中即可
2.2.3完整代码：
void merge(int nums1[], int m, int nums2[],int n)
{
//m、n是nums1/nums2有效数据个数
//nums1size是nums1数组长度
int l1 = m - 1;
int l2 = n - 1;
int l3 = m + n - 1;
while (l1 >= 0 && l2 >= 0)//注意这里的&&，只要有一个条件为假
{
if(nums1[l1] < nums2[l2])
{
nums1[l3--] = nums2[l2--];
}
else
{
nums1[l3--] = nums1[l1--];
}
}
//出了循环有两种情况：l1>=或者l2>=0,不可能存在l1和l2同时小于0
//如果l2>=0，说明l2还有数据没有完全放入l1中
while (l2 >= 0)
{
nums1[l3--] = nums2[l2--];
}
}
int main()
{
int nums1[10] = { 2,7,9 };
int nums2[] = { 1,3,5 };
int m = 3;
int n = 3;
merge(nums1,m,nums2, n);
printf("合并后的数组
");
for (int i = 0; i < m+n; i++)
{
printf("%d ", nums1[i]);
}
return 0;
}二、对顺序表的思考
顺序表作为数据结构的基础，虽然实现简单、随机访问效率高，但也存在一些明显的不足，主要体现在以下几个方面：
1. 插入/删除效率低
在中间或头部插入/删除元素时，需要移动后面的所有元素，时间复杂度为 O(n)。
当元素数量很大时，频繁的移动会导致性能显著下降。例如，在长度为1000的顺序表头部插入一个元素，需要移动999个元素。
2. 空间利用率不高
静态顺序表：容量固定，满了之后无法再插入新元素，容易造成空间浪费或溢出。
动态顺序表：扩容时需要重新分配更大的内存空间，并复制原有元素，会产生额外的时间开销。 扩容后的新空间可能有部分闲置，同样存在空间浪费的问题。
那么，针对以上问题如何解决呢？这就涉及到下一期的知识——链表，我们下期再见！
完。
如有任何错误，欢迎大家指正，我们共同进步！！
