【强化学习】REINFORCE 算法
目录
一、引言
二、REINFORCE 算法的核心定位与关键特性
三、REINFORCE 算法的数学基础（通俗推导，贴合代码）
1. 核心目标：最大化策略的期望累计回报
2. 关键推导：策略梯度的无偏估计
3. 工程化转化：梯度下降替代梯度上升
四、代码与算法的逐模块对应实现
模块 1：策略网络（PolicyNet）—— 实现策略πθ(a∣s)的参数化
模块 2：REINFORCE 算法核心类 —— 实现策略采样、累计回报计算、策略梯度更新
2.1 __init__：初始化算法核心组件
2.2 take_action：根据策略πθ(a∣s)采样动作（同策略探索）
2.3 update：REINFORCE 算法的核心 —— 实现蒙特卡洛策略梯度更新
模块 3：超参数与环境初始化 —— 工程化适配，保证实验可复现
模块 4：蒙特卡洛训练循环 —— 采集完整轨迹，实现回合式更新
模块 5：结果可视化 —— 分析训练收敛趋势
五、REINFORCE 算法的完整执行流程（结合代码）
六、REINFORCE 算法的Python代码完整实现
七、程序运行结果展示
八、REINFORCE 算法的优缺点（结合代码表现）
优点（代码完美体现）
缺点（代码训练中会体现）
九、经典改进方向（解决高方差 / 低效率问题）
十、总结
一、引言
REINFORCE 算法是策略梯度（Policy Gradient, PG） 家族中最经典、最基础的无模型强化学习算法，由 Williams 在 1992 年提出。核心特点是直接参数化策略、通过蒙特卡洛（MC）方式采集完整回合数据、用梯度上升最大化期望累计回报，区别于 DQN 这类先学习值函数再推导策略的 “间接法”，REINFORCE 是直接优化策略的 “直接法”，非常适合离散动作空间（如 CartPole-v1 的左右两个动作）。
二、REINFORCE 算法的核心定位与关键特性
先明确算法的核心属性，这是理解代码设计的基础，代码的每一处实现都贴合这些特性：
- 无模型（Model-Free）：无需学习环境的状态转移模型P(s′∣s,a)和奖励模型R(s,a)，仅通过与环境交互采集的轨迹数据更新策略，代码中仅用
env.step()和env.reset()交互，无任何环境模型相关代码。 - 同策略（On-Policy）：必须用当前策略采样的轨迹数据来更新策略，采样和更新的策略是同一个，代码中每回合用
agent.take_action()（当前策略）采样动作，采集完轨迹后直接用该轨迹更新策略，无经验回放（经验回放是异策略的典型特征）。 - 蒙特卡洛（MC）式更新：必须采集完整的回合轨迹（从初始状态到终止状态），只有拿到回合的全部奖励，才能计算每一步的累计折扣回报，代码中每个回合结束后才调用
agent.update()，而非步更 / 半回合更，这是蒙特卡洛的核心标志。 - 离散动作空间适配：策略网络输出动作的概率分布，通过类别分布（Categorical）采样动作，代码中用
torch.distributions.Categorical实现，完美适配 CartPole-v1 的二分类动作。 - 梯度上升最大化回报：目标是找到策略参数，让策略的期望累计回报最大；因 PyTorch 仅支持梯度下降，故将 “最大化回报” 转化为 “最小化负的回报损失”，代码中损失函数为
- log_prob * G就是这个逻辑。
三、REINFORCE 算法的数学基础（通俗推导，贴合代码）
REINFORCE 的核心是推导出策略梯度的无偏估计，让代码的更新逻辑有理论支撑。
1. 核心目标：最大化策略的期望累计回报
我们用参数θ表示策略网络（代码中是 PolicyNet 的权重），策略记为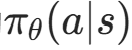
，表示在状态s下，策略θ选择动作a的概率。
算法的核心目标是找到最优参数θ∗，让策略的期望累计折扣回报J(θ)最大：
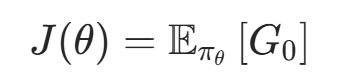
其中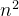
是从初始状态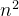开始的累计折扣回报，
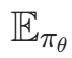表示对策略
采样的所有轨迹求期望。
2. 关键推导：策略梯度的无偏估计
要最大化J(θ)，需要计算J(θ)对参数θ的梯度
（即策略梯度），然后用梯度上升更新θ：
（α是学习率，代码中由 Adam 优化器自适应调整）
Williams 通过数学推导，得出策略梯度的无偏蒙特卡洛估计（这是 REINFORCE 的核心公式）：
- N：训练的回合数（代码中每次 update 对应 1 个回合，N=1）；
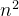- ：第n个回合的步数；
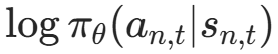：第n回合t步，策略选择动作an,t的对数概率（代码中log_prob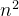）；- ,t：第n回合t步开始到回合结束的累计折扣回报（代码中
G），计算式为：
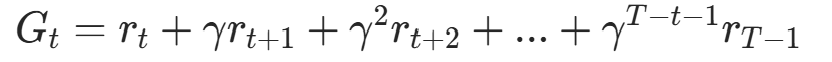
是折扣因子（代码中gamma=0.98），用于衰减远期奖励的权重，让算法更关注近期奖励。
3. 工程化转化：梯度下降替代梯度上升
PyTorch 等深度学习框架仅支持梯度下降（最小化损失函数），因此将策略梯度的最大化目标转化为最小化负的策略梯度损失：
这就是代码中loss = - log_prob * G的理论根源，反向传播该损失的梯度，等价于对原目标做梯度上升。
四、代码与算法的逐模块对应实现
代码分为策略网络（PolicyNet）、REINFORCE 算法核心类、超参数与环境初始化、蒙特卡洛训练循环、结果可视化5 个模块，每个模块都严格对应 REINFORCE 算法的理论要求，下面逐模块讲解。
模块 1：策略网络（PolicyNet）—— 实现策略πθ(a∣s)的参数化
策略网络是 REINFORCE 的 “核心载体”，作用是将状态s映射为动作a的概率分布，代码中是两层全连接网络，适配 CartPole-v1 的简单状态空间（4 维观测）。
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim) # 状态映射到隐藏层
self.fc2 = torch.nn.Linear(hidden_dim, action_dim) # 隐藏层映射到动作空间
def forward(self, x):
x = F.relu(self.fc1(x)) # 非线性激活，拟合复杂状态-动作映射
return F.softmax(self.fc2(x), dim=1) # 转概率分布（和为1）
算法对应点：
- 输入
state_dim（CartPole-v1 为 4）：环境的观测维度，对应状态s； - 输出
action_dim（CartPole-v1 为 2）：离散动作的数量，输出值经softmax激活后，直接表示πθ(a∣s)（状态s下选每个动作的概率）； softmax的必要性：保证输出是合法的概率分布（所有动作的概率和为 1），这是策略πθ(a∣s)的基本要求。
模块 2：REINFORCE 算法核心类 —— 实现策略采样、累计回报计算、策略梯度更新
这是代码的核心，完全实现了 REINFORCE 的三大核心功能：动作采样、累计折扣回报Gt计算、策略梯度更新，分为__init__、take_action、update三个方法。
2.1 __init__：初始化算法核心组件
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, device):
self.policy_net = PolicyNet(state_dim, hidden_dim, action_dim).to(device) # 策略网络
self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=learning_rate) # 梯度优化器
self.gamma = gamma # 折扣因子γ，用于计算G_t
self.device = device # 训练设备（GPU/CPU）
关键细节：用 Adam 自适应优化器替代原始的随机梯度上升（SGD），提升训练稳定性和收敛速度，这是工程实现的常规优化，不改变算法核心。
2.2 take_action：根据策略πθ(a∣s)采样动作（同策略探索）
def take_action(self, state):
# 状态转张量，消除创建警告，适配设备
state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)
probs = self.policy_net(state) # 得到动作概率分布π_θ(a|s)
action_dist = torch.distributions.Categorical(probs) # 构建类别分布
action = action_dist.sample() # 从概率分布中随机采样动作
return action.item()
算法对应点：
- 非贪心采样：策略梯度算法需要探索环境，因此不能选概率最大的动作（贪心），而是从概率分布中随机采样（比如动作 1 概率 0.8、动作 2 概率 0.2，大概率选 1 但小概率选 2，保证探索）；
- 类别分布（Categorical）：专门用于离散动作的概率采样，输入动作概率分布，输出采样的动作索引，完美适配 REINFORCE 的离散动作要求；
- 同策略采样：每次采样用的都是当前策略网络的最新参数，符合 “同策略” 特性。
2.3 update：REINFORCE 算法的核心 —— 实现蒙特卡洛策略梯度更新
这部分代码完全对应策略梯度的数学公式，是算法的 “灵魂”，必须在采集完完整回合轨迹后调用。
def update(self, transition_dict):
# 从轨迹字典中取出当前回合的所有s/a/r
reward_list = transition_dict['rewards']
state_list = transition_dict['states']
action_list = transition_dict['actions']
G = 0 # 初始化累计折扣回报
self.optimizer.zero_grad() # 清空梯度（PyTorch梯度累加，必须手动清空）
# 从最后一步反向遍历，计算每一步的G_t（核心！）
for i in reversed(range(len(reward_list))):
reward = reward_list[i] # 当前步的奖励r_t
# 状态转张量，适配设备
state = torch.tensor(np.array([state_list[i]]), dtype=torch.float).to(self.device)
# 动作转张量并reshape，匹配gather的维度要求
action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
# 计算log π_θ(a_t|s_t)：取当前动作对应的对数概率
log_prob = torch.log(self.policy_net(state).gather(1, action))
# 反向计算累计折扣回报G_t = r_t + γ * G_{t+1}
G = self.gamma * G + reward
# 计算单步损失：- log_prob * G（梯度下降替代梯度上升）
loss = - log_prob * G
loss.backward() # 单步反向传播，累加梯度（核心！逐步计算，梯度累加）
self.optimizer.step() # 一次更新所有参数（同策略MC的特性）
算法核心细节（逐行对应理论）：
- 反向遍历计算Gt：从回合最后一步（t=T−1）往回算，是计算累计折扣回报最高效的方式，公式为
：
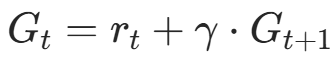- 最后一步（t=T−1）：
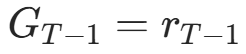（后面无奖励，G=0）； - 倒数第二步（t=T−2）：
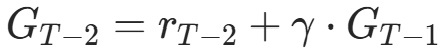； - 以此类推，直到第一步（t=0），完美计算每一步的
。
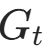- 最后一步（t=T−1）：
gather(1, action)：从策略网络输出的动作概率分布中，取出当前采样动作对应的概率（比如输出 [0.2, 0.8]，采样动作 1，就取 0.8），再取对数得到
。- 梯度累加（
loss.backward()在循环内）：策略梯度的公式是所有步的梯度之和，因此这里逐步计算损失并反向传播，让 PyTorch 自动累加梯度，最后一次更新参数，这是 REINFORCE 蒙特卡洛更新的标准实现。 - 一次更新参数（
optimizer.step()在循环外）：遍历完所有步、累加完所有梯度后，才调用优化器更新策略网络的参数，符合 “完整回合后更新” 的蒙特卡洛特性。
模块 3：超参数与环境初始化 —— 工程化适配，保证实验可复现
这部分是强化学习的工程实现基础，无算法理论，但直接影响训练效果和实验可复现性，代码中做了 Gymnasium 的完整适配。
# 超参数设置
learning_rate = 1e-3 # 学习率
num_episodes = 1000 # 总训练回合数
hidden_dim = 128 # 策略网络隐藏层维度
gamma = 0.98 # 折扣因子γ
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu") # 自动选设备
# 环境初始化（Gymnasium适配）
env_name = "CartPole-v1"
# 设置全局随机种子，保证实验可复现
np.random.seed(0)
torch.manual_seed(0)
random.seed(0)
env = gym.make(env_name)
# Gymnasium移除env.seed()，改用动作/观测空间种子
env.action_space.seed(0)
env.observation_space.seed(0)
# 获取环境维度
state_dim = env.observation_space.shape[0] # 状态维度：4
action_dim = env.action_space.n # 动作维度：2
# 实例化REINFORCE智能体
agent = REINFORCE(state_dim, hidden_dim, action_dim, learning_rate, gamma, device)
关键工程细节：
- 随机种子设置：强化学习的训练结果受随机采样（动作、环境）影响，设置种子后，每次训练的结果完全一致，方便调参和验证；
- Gymnasium 适配：Gym 自 2022 年废弃，Gymnasium 是官方无缝替代，代码中处理了
reset/step的返回值变化（后续训练循环会详细讲）； - 设备自适应：自动选择 GPU（如果有）加速训练，无 GPU 则用 CPU，不影响算法逻辑。
模块 4：蒙特卡洛训练循环 —— 采集完整轨迹，实现回合式更新
这部分代码实现REINFORCE 的蒙特卡洛核心要求：与环境交互，采集完整的回合轨迹，存储所有s/a/r/s′/done，回合结束后调用agent.update()更新策略，是 “算法理论” 到 “环境交互” 的桥梁。
return_list = [] # 存储每个回合的总回报，用于可视化
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0 # 存储当前回合的总回报
# 轨迹字典：存储当前回合的所有s/a/r/s'/done（蒙特卡洛需要完整轨迹）
transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
state, _ = env.reset(seed=0) # Gymnasium：reset返回(state, info)
done = False
while not done:
action = agent.take_action(state) # 同策略采样动作
# Gymnasium：step返回(next_state, reward, terminated, truncated, info)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated # 合并终止状态（环境终止+步数截断）
# 存储当前步的轨迹数据
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
# 更新状态和当前回合总回报
state = next_state
episode_return += reward
# 回合结束：存储总回报，调用update更新策略（蒙特卡洛核心！）
return_list.append(episode_return)
agent.update(transition_dict)
# 每10回合打印平均回报，监控训练进度
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
'return': '%.3f' % np.mean(return_list[-10:])})
pbar.update(1)
算法与工程对应点：
- 完整轨迹采集：
while not done循环直到回合终止，保证采集的是从初始状态到终止状态的完整轨迹，符合蒙特卡洛 “完整回合更新” 的要求； - Gymnasium 适配：处理了 Gymnasium 与原 Gym 的返回值差异（核心工程适配，不影响算法）：
env.reset(seed=0)：返回(state, info)，取第一个元素为状态；env.step(action)：返回(next_state, reward, terminated, truncated, info)，其中terminated是环境自然终止（如 CartPole 倒了），truncated是步数截断（如 CartPole 撑到 500 步），合并为done表示回合结束；
- 回合式更新：只有当
while not done循环结束（回合终止），才调用agent.update(transition_dict)，将完整轨迹传入更新策略，这是 REINFORCE 蒙特卡洛特性的核心工程实现； - 回报监控：用
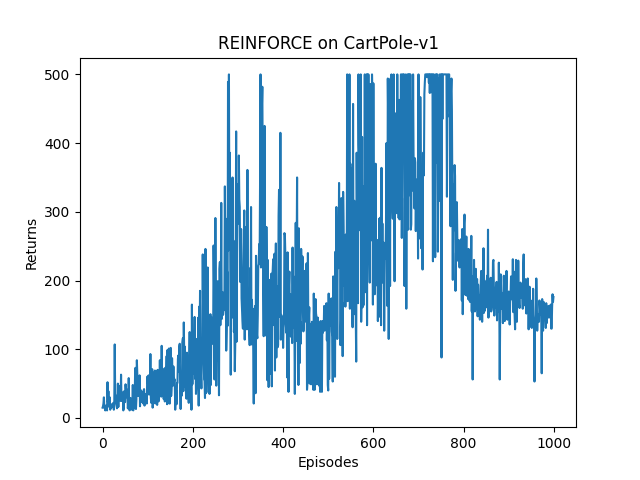
return_list存储每个回合的总回报，每 10 回合计算一次平均回报，用于监控训练收敛趋势（CartPole-v1 的最大回报是 500，平均回报稳定在 500 表示算法收敛）。
模块 5：结果可视化 —— 分析训练收敛趋势
强化学习的训练过程存在大量噪声（因动作是随机采样的），直接绘制原始回报曲线会波动剧烈，因此代码中绘制了原始回报曲线和移动平均（Moving Average）回报曲线，后者用于平滑噪声，清晰展示收敛趋势。
# 绘制原始回报曲线并保存
episode_list = list(range(len(return_list)))
plt.plot(episode_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.savefig('REINFORCE on CartPole-v1_training.png')
plt.show()
# 绘制移动平均回报曲线并保存（窗口大小9，平滑噪声）
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episode_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Moving Average Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.savefig('REINFORCE on CartPole-v1_moving_average.png')
plt.show()
关键作用：
- 原始回报曲线：展示每回合的真实训练效果，能看到噪声波动；
- 移动平均曲线：用
rl_utils.moving_average计算窗口内的平均回报，平滑噪声，能清晰看到算法是否收敛、收敛速度、收敛稳定性（比如 CartPole-v1 的移动平均曲线会逐渐上升，最终稳定在 500）。
五、REINFORCE 算法的完整执行流程（结合代码）
将上述模块串联，代码的执行流程就是 REINFORCE 算法的标准执行流程，一步一步清晰明了：
- 初始化：创建 CartPole-v1 环境，初始化策略网络和 REINFORCE 智能体，设置超参数和随机种子；
- 循环训练回合：总共有 1000 个训练回合，分 10 次迭代，每次 100 回合；
- 采集完整轨迹：对每个回合，从
env.reset()开始，用当前策略agent.take_action()采样动作，通过env.step()与环境交互，采集每一步的s/a/r/s′/done，直到回合终止，得到完整轨迹； - 蒙特卡洛策略梯度更新：回合终止后，将完整轨迹传入
agent.update()，反向计算每一步的累计折扣回报Gt，计算策略梯度并累加，最后一次更新策略网络的参数； - 监控训练进度：存储每个回合的总回报，每 10 回合打印平均回报，监控收敛趋势；
- 可视化结果：训练结束后，绘制原始回报曲线和移动平均回报曲线，分析算法收敛效果；
- 收敛标志：当 CartPole-v1 的回合平均回报稳定在 500（环境最大步数），表示策略收敛，智能体能稳定让小车保持平衡。
六、REINFORCE 算法的Python代码完整实现
先实现rl_utils库，它包含一些函数，如绘制移动平均曲线、计算优势函数等，不同的算法可以一起使用这些函数。
rl_utils.py中的Python代码如下：
from tqdm import tqdm
import numpy as np
import torch
import collections
import random
class ReplayBuffer:
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity)
def add(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size):
transitions = random.sample(self.buffer, batch_size)
state, action, reward, next_state, done = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), done
def size(self):
return len(self.buffer)
def moving_average(a, window_size):
cumulative_sum = np.cumsum(np.insert(a, 0, 0))
middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
r = np.arange(1, window_size - 1, 2)
begin = np.cumsum(a[:window_size - 1])[::2] / r
end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
return np.concatenate((begin, middle, end))
def train_on_policy_agent(env, agent, num_episodes):
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
state, _ = env.reset() # 适配Gymnasium：reset返回(state, info)
done = False
while not done:
action = agent.take_action(state)
# 适配Gymnasium：step返回(next_state, reward, terminated, truncated, info)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated # 终止=环境终止+步数截断
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
state = next_state
episode_return += reward
return_list.append(episode_return)
agent.update(transition_dict)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
'return': '%.3f' % np.mean(return_list[-10:])})
pbar.update(1)
return return_list
def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
state, _ = env.reset() # 适配Gymnasium
done = False
while not done:
action = agent.take_action(state)
# 适配Gymnasium step返回值
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r,
'dones': b_d}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
'return': '%.3f' % np.mean(return_list[-10:])})
pbar.update(1)
return return_list
def compute_advantage(gamma, lmbda, td_delta):
td_delta = td_delta.detach().numpy()
advantage_list = []
advantage = 0.0
for delta in td_delta[::-1]:
advantage = gamma * lmbda * advantage + delta
advantage_list.append(advantage)
advantage_list.reverse()
return torch.tensor(advantage_list, dtype=torch.float)
REINFORCE 算法的Python代码如下：
import gymnasium as gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import rl_utils
import random # 用于设置全局随机种子
from tqdm import tqdm
# 策略网络
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
# REINFORCE算法
class REINFORCE:
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, device):
self.policy_net = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=learning_rate)
self.gamma = gamma
self.device = device
def take_action(self, state):
state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)
probs = self.policy_net(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
reward_list = transition_dict['rewards']
state_list = transition_dict['states']
action_list = transition_dict['actions']
G = 0
self.optimizer.zero_grad()
# 从最后一步反向计算累计回报
for i in reversed(range(len(reward_list))):
reward = reward_list[i]
state = torch.tensor(np.array([state_list[i]]), dtype=torch.float).to(self.device)
action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
log_prob = torch.log(self.policy_net(state).gather(1, action))
G = self.gamma * G + reward
loss = - log_prob * G # 损失为负的对数概率乘累计回报（梯度上升等价于损失下降）
loss.backward() # 逐步反向传播计算梯度
self.optimizer.step() # 一次更新所有参数（同策略算法特性）
# 超参数设置
learning_rate = 1e-3
num_episodes = 1000 # 总训练回合数，原代码循环分10次，每次100回合，匹配总次数
hidden_dim = 128
gamma = 0.98
# 自动选择GPU/CPU
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
# 环境初始化
env_name = "CartPole-v1"
# 设置全局随机种子（保证实验可复现）
np.random.seed(0)
torch.manual_seed(0)
random.seed(0)
# 创建环境，设置环境种子
env = gym.make(env_name)
env.action_space.seed(0)
env.observation_space.seed(0)
# 获取环境维度
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
# 实例化REINFORCE智能体
agent = REINFORCE(state_dim, hidden_dim, action_dim, learning_rate, gamma, device)
# 训练循环
return_list = []
for i in range(10):
# 总回合数1000，分10次迭代，每次100回合
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
# 适配Gymnasium：reset返回(state, info)，取第一个元素
state, _ = env.reset(seed=0) # 重置时指定seed
done = False
while not done:
action = agent.take_action(state)
# 适配Gymnasium：step返回(next_state, reward, terminated, truncated, info)
next_state, reward, terminated, truncated, _ = env.step(action)
# Gymnasium将done拆分为terminated（环境终止）和truncated（步数截断），合并为done
done = terminated or truncated
# 存储转移数据
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
# 更新状态和累计回报
state = next_state
episode_return += reward
# 存储当前回合回报
return_list.append(episode_return)
# 更新策略网络
agent.update(transition_dict)
# 每10回合打印一次平均回报
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
'return': '%.3f' % np.mean(return_list[-10:])})
pbar.update(1)
# 绘制训练曲线
episode_list = list(range(len(return_list)))
plt.plot(episode_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.savefig('REINFORCE on CartPole-v1_training.png')
plt.show()
# 绘制移动平均曲线，平滑显示训练趋势
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episode_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Moving Average Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.savefig('REINFORCE on CartPole-v1_moving_average.png')
plt.show()
七、程序运行结果展示
Iteration 0: 100%|██████████| 100/100 [00:01<00:00, 77.79it/s, episode=100, return=32.300]
Iteration 1: 100%|██████████| 100/100 [00:02<00:00, 42.19it/s, episode=200, return=65.400]
Iteration 2: 100%|██████████| 100/100 [00:06<00:00, 15.55it/s, episode=300, return=200.400]
Iteration 3: 100%|██████████| 100/100 [00:08<00:00, 11.99it/s, episode=400, return=213.200]
Iteration 4: 100%|██████████| 100/100 [00:06<00:00, 16.56it/s, episode=500, return=130.000]
Iteration 5: 100%|██████████| 100/100 [00:10<00:00, 9.25it/s, episode=600, return=343.400]
Iteration 6: 100%|██████████| 100/100 [00:14<00:00, 6.99it/s, episode=700, return=319.700]
Iteration 7: 100%|██████████| 100/100 [00:17<00:00, 5.80it/s, episode=800, return=224.100]
Iteration 8: 100%|██████████| 100/100 [00:08<00:00, 12.45it/s, episode=900, return=176.100]
Iteration 9: 100%|██████████| 100/100 [00:07<00:00, 14.16it/s, episode=1000, return=158.500]
八、REINFORCE 算法的优缺点（结合代码表现）
优点（代码完美体现）
- 直接优化策略：无需学习值函数，直接参数化并优化策略，策略表达更灵活，既适合离散动作空间（如本代码），也可轻松适配连续动作空间（改策略网络输出和采样分布即可，如用正态分布采样连续动作）；
- 实现简单：核心逻辑仅 “采样轨迹 - 计算 G_t - 更新策略” 三步，代码量少，无复杂的值函数拟合、目标网络等模块；
- 无偏估计：蒙特卡洛方式用完整回合的回报计算Gt，是策略梯度的无偏估计，训练收敛后策略的性能更稳定。
缺点（代码训练中会体现）
- 高方差：蒙特卡洛的无偏估计伴随高方差，导致训练回报曲线波动剧烈，收敛速度慢（本代码中训练前期回报波动大，后期才逐渐收敛）；
- 同策略效率低：必须用当前策略采样的轨迹更新，采样的轨迹用过一次就丢弃，不能复用（如 DQN 的经验回放），数据利用率极低；
- 只能回合更新：必须等回合结束才能更新，无法进行步更 / 半回合更，对长回合任务（如 Atari 游戏）训练效率极低；
- 无探索 - 利用平衡的显式控制：仅通过动作概率采样实现探索，无专门的探索机制（如 ε- 贪心），探索策略较粗糙。
九、经典改进方向（解决高方差 / 低效率问题）
针对 REINFORCE 的缺点，后续有很多经典改进版，都是工业界常用的策略梯度算法：
- REINFORCE with Baseline：引入值函数作为基线（Baseline），将损失改为−logprob⋅(Gt−V(st))，大幅降低方差，不改变无偏性；
- Actor-Critic（AC）：结合策略梯度（Actor）和值函数（Critic），用 TD 误差替代蒙特卡洛的Gt，实现步更 / 半回合更，提升训练效率；
- A2C/A3C：在 AC 基础上做并行训练，进一步提升训练速度；
- PPO（Proximal Policy Optimization）：当前最主流的策略梯度算法，在同策略的基础上引入信任域，允许轨迹复用，兼顾效率和稳定性，是工业界的 “首选方案”。
十、总结
本文详细介绍了REINFORCE算法的原理与实现。REINFORCE是一种基于策略梯度的无模型强化学习算法，直接优化策略参数，适用于离散动作空间。文章从算法定位、数学推导、代码实现三个层面展开：首先阐述了其无模型、同策略、蒙特卡洛更新的核心特性；然后推导了策略梯度的数学公式及其工程化实现；最后通过完整的Python代码展示了在CartPole-v1环境中的应用，包括策略网络设计、轨迹采集、蒙特卡洛更新等关键模块。实验结果表明，REINFORCE算法能够有效解决简单控制问题，但存在高方差、低效率等缺点。文章还指出了改进方向，如引入基线函数、Actor-Critic架构等。整体上，REINFORCE作为策略梯度家族的基础算法，具有理论简洁、实现直观的特点。
