基于K-means聚类的快递选址和最短路径规划
基于K-means聚类的快递选址和最短路径规划
- 摘要
- 一、K-means聚类算法
- 二、蚁群算法
- 2.1路径构建
- 2.2信息素更新
- 三.仿真
- 总结
摘要
`
针对当前多区域物流中心选址需建立配送中心个数不定、位置、覆盖范围不明的问题,本文提出了一种改进的k-means 聚类算法, 根据每个快递点的地理位置进行聚类划分,分别在这些区域网点中对配送中心进行最终的确定。之后,以一类区域网点为例,采用遗传算法对遍历网点的最短路程进行规划,提供参考。
提示:以下是本篇文章正文内容,下面案例可供参考
一、K-means聚类算法
K-means原理是初始随机给定k个簇中心,在未知样本类别的情况下,通过计算样本间的距离(欧式距离、马式距离、汉明距离、余弦距离等)来估计样本所属类别。把待分类样本点按照最邻近原则划分到不同的簇后,按平均法再一次计算每个簇的质心得到新的簇心,重复迭代,当簇心的移动距离小于某个给定的值时才停止。
从图中可以看出,所给数据集经过迭代后,最终形成了三个较为良好的簇类。
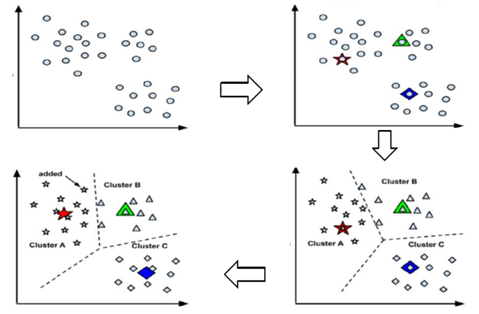
二、蚁群算法
蚁群算法求解旅行商问题大致可以分为两步:
2.1路径构建

2.2信息素更新

三.仿真
使用python生成100个范围在[0,1]随机坐标作为网点坐标

K—means聚类分析:

以粉色坐标点为例,采用蚁群算法设计遍历网点的最短路径。

总结为如下内容

总结
本文以配送中心选址为研究对象,生成了100个随机网点,研究配送中心选址策略,完成了以下几项主要工作:
第一,设计了基于K-means的聚类分析方法,将100个随机网点分为五类并生成了5个配送中心。
第二,以其中一类网点为例,基于蚁群算法设计了配送的最短路径。
具体代码可以参考我的资源,觉得有用的小伙伴点赞关注。











