开关电源设计概述
1. 环路分析与设计课程导论
环路分析与设计”系列课程的第一步,旨在为后续学习打下坚实的数学与概念基础。课程强调从物理意义出发理解数学工具,而非仅进行形式化推导。
2. 课程目标与内容概览
课程的主要目标包括:
- 对环路分析与设计建立整体认知;
- 通过实例说明环路部分对输出电压的影响;
- 明确环路稳定性的基本要求;
- 引入传递函数(Transfer Function) 的概念与定义;
- 通过实际例子演示如何在时域(time domain) 中求解传递函数;
- 介绍后续所需的数学工具及其物理背景。
3. 数学函数的物理意义与应用背景
强调:所有数学函数的提出都源于实际问题,并非凭空构造。理解其物理背景有助于降低学习难度并增强直觉。
常见函数及其物理意义:
-
正弦函数(Sine Function)
用于描述周期性现象(如交流电压、电流)。
特殊性质:对正弦函数求导或积分,结果仍是同频率的正弦或余弦函数,仅相位偏移 90°
例如:
-
指数函数(Exponential Function)
自然界中许多过程遵循指数规律,如电容充电/放电:
其中 τ=RC 为时间常数。
-
以 e为底的指数函数(e^x)
具有独特性质:其导数和积分仍为自身: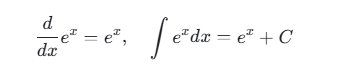
这一性质极大简化了微分方程的求解,在系统分析中极为重要。
-
对数函数(Logarithmic Function)
作为指数的反运算,核心优势在于将乘除运算转化为加减运算:
进一步地,可将非线性关系线性化(如将幂律曲线变为直线),这正是波特图(Bode Plot)采用对数坐标的根本原因。
4. 微分的物理含义:扰动与稳定性
- 数学上的微分 ↔ 物理上的扰动(perturbation)。
- 环路稳定性研究的核心是:系统对微小输入波动的响应是否收敛。
- 若系统对任意微小扰动都能恢复稳态,则称其稳定;否则不稳定。
- 因此,微分不仅是数学操作,更是分析系统动态行为的关键工具。
5. 相量表示法(Phasor Representation)
- 正弦信号
 需用幅值、频率、相位三个参数完整描述。
需用幅值、频率、相位三个参数完整描述。 - 当频率固定时,可使用相量(Phasor) 表示:

- 相量在复平面上表示,便于进行代数运算(如加法、乘法),远比时域波形叠加简便。
- 相量法是频域分析的基础工具之一。
6. 傅里叶变换(Fourier Transform)的物理意义
- 核心思想:任意随时间变化的信号(满足一定条件)可分解为多个不同频率的正弦分量的叠加。
- 通过图形化方式(如频谱图)可直观展示各频率成分的幅值与相位。
- 实现了从时域分析到频域分析的转换:
- 时域:研究单一复杂信号;
- 频域:研究多个简单正弦分量的组合。
- 傅里叶变换是理解系统频率响应的前提。
7. 拉普拉斯变换(Laplace Transform)及其在电路分析中的应用
- 拉普拉斯变换是傅里叶变换的推广,适用于更广泛的信号(包括非周期、增长信号)。
- 定义(单边):

- 在电路分析中,拉普拉斯变换可将微分方程转化为代数方程,极大简化求解过程。
- 传递函数 H(s)即在 s 域中定义的输出与输入之比:

- 整个课程将在频域(s 域) 中展开,因此掌握拉普拉斯变换至关重要。

本文地址:https://www.yitenyun.com/6843.html
下一篇:宁波庭院门厂家哪家专业?












