再论自然数全加和-质数公式和哥德巴赫猜想
再回到黎曼泽塔函数，
它的周期性实际含义为，
如果 
是 
的下一个质数，
回顾 
的情况，
得到，关于 
的一次和二次方程，
观察这个结果，
另外，
可见这里的，
反过来代入，
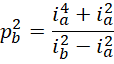
列出一次和二次方程，
对一次方程平方，
由这个方程可以解出非常复杂的结果（8次方），但由于我们只需要，
所以，设，
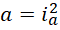
解法如下，由于是4次方程，解为4个根，
所以，
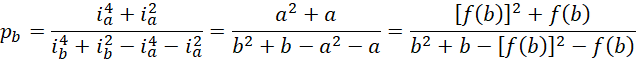
这就是给定虚数单位，得到对应的质数的公式。 
作为方程的解，有两个实根两个虚根，其中 
会导致分母为0，所以实根只有一个，而且非常复杂。
现在考虑两个质数的和，
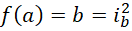
也就是说，
其中 
为周期。所以任何一个偶数总能写成两个质数之和的形式（如果质数包括1，则结果包括2，但方程有两项其中一项的系数已经为2，另一项不等于0，所以这里的质数不包括1），由此哥德巴赫猜想得证。
